In a very real sense, mathematics is the key to physics. We can get a qualitative understanding of physical events like accelerating, heating, electric circuits, laser, nuclear energy, etc. without using much maths. Like when we visit a science centre or museum. But if we need a deeper understanding of physics, whether to build new high tech devices or take physics exams, we need to make use of mathematics.
This article summarises all the mathematics requirement listed in the A level physics syllabus in Singapore for 2024. The mathematics required for O level physics is less demanding, consisting of a scaled down level of algebra, geometry and trigonometry, and graphs only.
Arithmetic
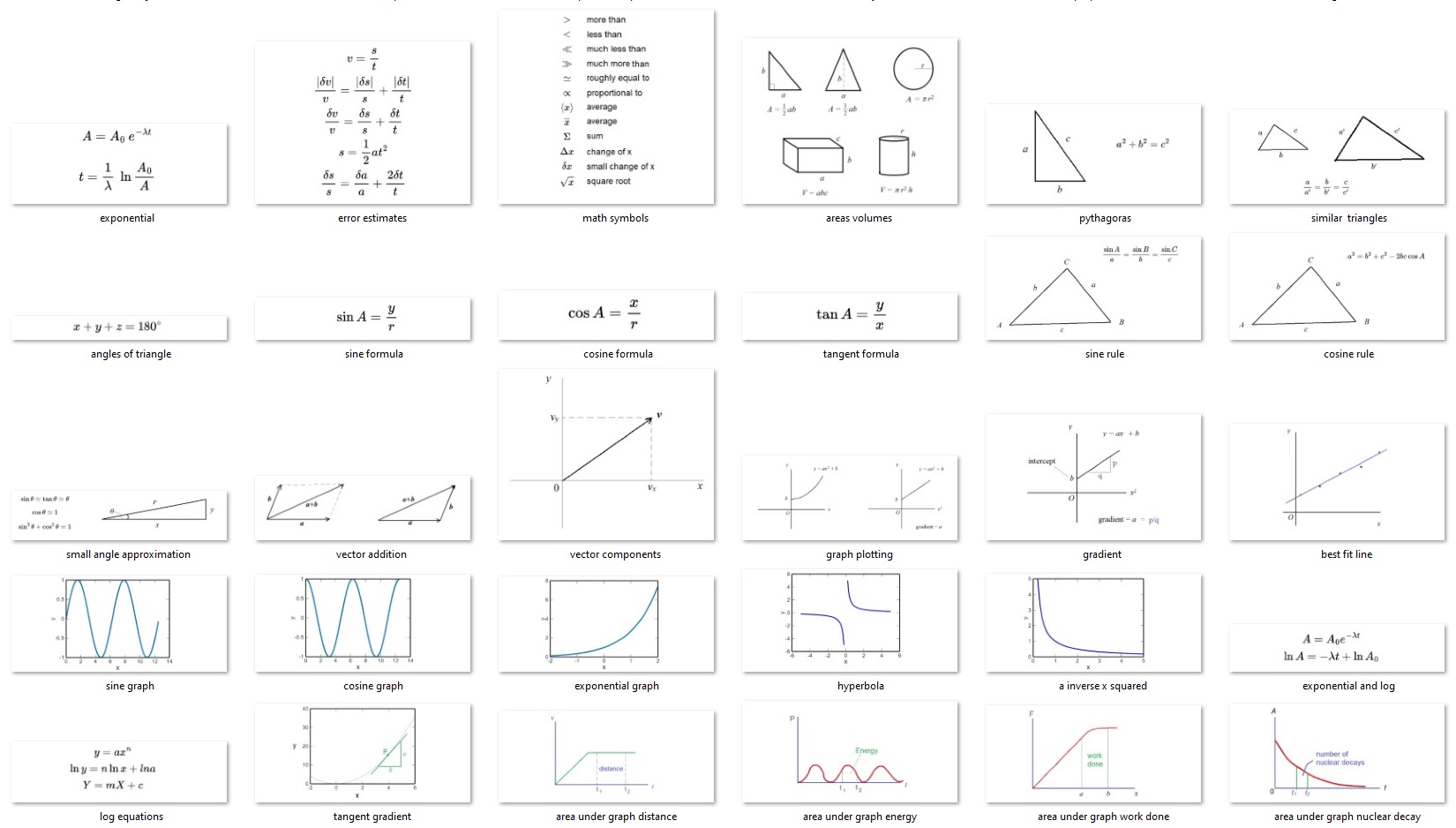
This first number is called Avogadro constant. It is a huge number, roughly roughly 6 followed by 23 zeros. It is used as a unit for the number of atoms or molecules in a substance. For example, 12 g of carbon has this number of carbon atoms.
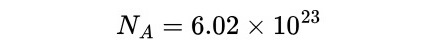
The next mathematical item we need to know, not surprisingly, is the calculator. Who does not need one these days? But if you look more carefully at this image, you can see that it is a bit different from the calculator we see on shop counters. It has many wierd symbols that shopkeepers would be happy not to use, like sine, cosine, square root, etc. This makes it somewhat complicated and does take practice to get used to.

You may know that to measure the size of an angle, we use a protractor to see how many degrees the angle is. We do use degrees in physics, but we also have to use another unit of angle called radian.
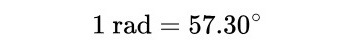
The unit of radian may seem quite wierd at first. 1 radian is 57.30 degrees. Why would anyone want to use such a unit?
The reason is actually quite simple. The radian unit makes it easier to calculate distance travelled along a circle. This is important when we need to study the motion of planets and satellites.
For more down to earth uses, we also need it if we need to design or build any device or motion that go round in circles.
In physics, we often have to measure things. Things like length, mass, time, energy, ... We may like the measurement to be as accurate as possible. But we have to be careful about carrying this too far. Suppose that someone decides to measure his height super accurately - to 10 decimal places! After a lot of work and spending a lot of money on super precise high tech laser instruments, he happily found his height to 10 decimal places:
For the rest of us, my guess is that we would be quite satisfied by 2 decimal places, like 1.63 m. In physics, we have to learn to decide what is the suitable accuracy to use.
There are also times when less accurate calculations can be useful. One example is when you have just calculated the answer from a complex formula using your calculator. Now it is quite easy to press a wrong button without noticing, especially under exam conditions, and end up with an answer that is way off.
Rather than repeating the calculation, a quick way would be to approximate the each number to one figure, like 320 is roughly 300, and repeating the calculation to see if the answer is not off by a million times. Here is an interesting example given in the syllabus.
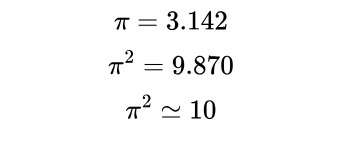
What the syllabus is suggesting is that if you have a complex formula that has π2 inside, you should repeat the calculation with π2 replaced by 10. If the answer is just off by a few percent from your actual answer, that you are probably right.
Algebra
Some knowledge of algebra is needed for physics. This include basic algebra, logarithms and exponentials.
For example, this is the formula for calculating the distance travelled by a car that is accelerating uniformly. This means the car's velocity increases by the same amount every second.
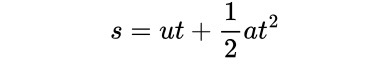
Suppose that a question gives us the values of the initial velocity u, time taken t, distance travelled s, and wants us to find the acceleration. Then we have to rearrange the equation so that the acceleration appears on the left hand side of the equation. Like this.
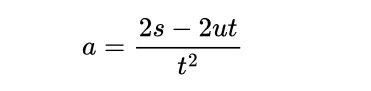
Suppose, however, that they twisted the question and wants us to find the time travelled instead. Notice that the unknown time t in the equation has both t and t2. This type of equation is called a quadratic equation. In order to solve this for the time t, we need to know this formula for the roots (meaning answers) of the quadratic equation. Like this.
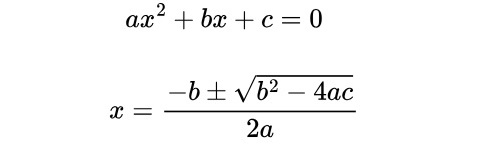
Another type of maths equations we need to know how to solve is simultaneous equations. It looks like the two equations below, where we have 2 unknowns x and y to solve for. An example of such calculation is to find the time and place where a car overtakes another car, both travelling at steady speed.
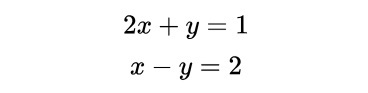
Belatedly, here is the formula for velocity. It looks like the usual distance over time for speed. It can be. But with a small twist, the word "velocity" is loaded with an additional meaning - direction. And s, which looks like distance, can also be loaded with direction info - and given a new name "displacement". And direction info can simply be included by adding + or - signs to v and s.
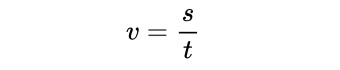
Next, we look at the use of physics with mathematics to understand accleration and deceleration in the real world. It can be a car accelerating at constant rate. It can be a stone falling through water against water resistance. From many experiments of scientists, we know that the variation in velocity are often similar the these equations.
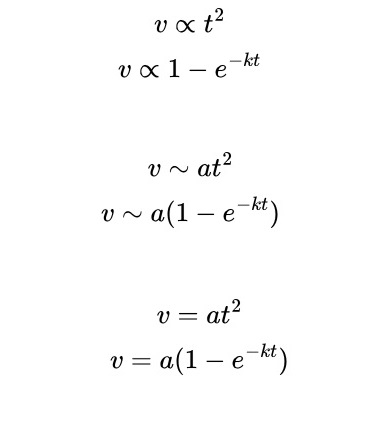
The symbols above relating the left and right sides of the 3 pairs of equations above are respectively proportional (∝ ), approximate (~), and equal (=).
The next thing we need to know is logarithm. After so many years of working with physics and maths, I still find logarithms rather strange. See for yourself!
It is easier to start with something familiar, like power of 10. For example, 10 to the power of 2, or 102, is 100. Now lets turn this around and ask: 100 is 10 to the power of what? We already know the answer is 2.
The question
"100 is 10 to the power of what?",
is exactly the same as
"what is the logarithm of 100 to base 10?".
The answer to both question is 2.
If you are new to this, I hope this can give you some idea of what logarithm means, if you are not totally confused by now.
The following list of equations are basically all the logarithm mathematics you need to know.
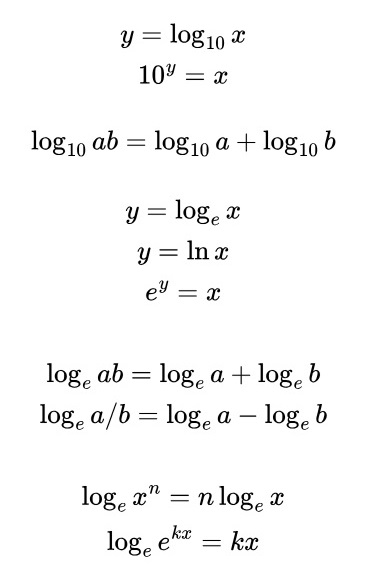
If you have looked, you would notice that apart from the first 3 equations in the list above, the rest have changed from base 10 to base e. What is e? Answer: e = 2.71828... Why do we have to bring in this weird number? Because it naturally when we solve physics equations for many things in nature, like stone falling through air and radioactive decay. Here is another way to write it.
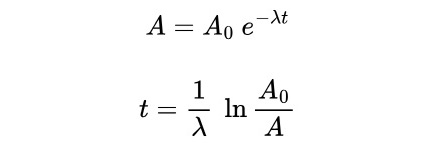
The mathematics of logarithm leads on to formulae used in at least 2 important topics in this syllabus - error analysis, and radioactive decay. Thankfully, students would not be directly tested on this in exams, but having a good understanding would definitely help.
The following are some examples of the kind of expressions we get when we do error analysis - to estimate errors when we use measured quantities to do calculations in physics.
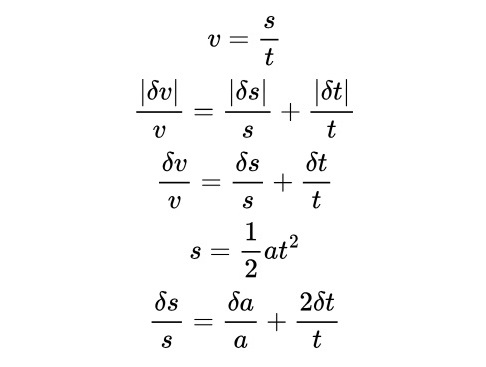
The following is a list of maths symbols needed for A level physics. A few of them I seldom see in exam papers, like the >> sign. But since it is listed in the syllabus, it is worth going through the list to make sure you know all of them.

Geometry and trigonometry
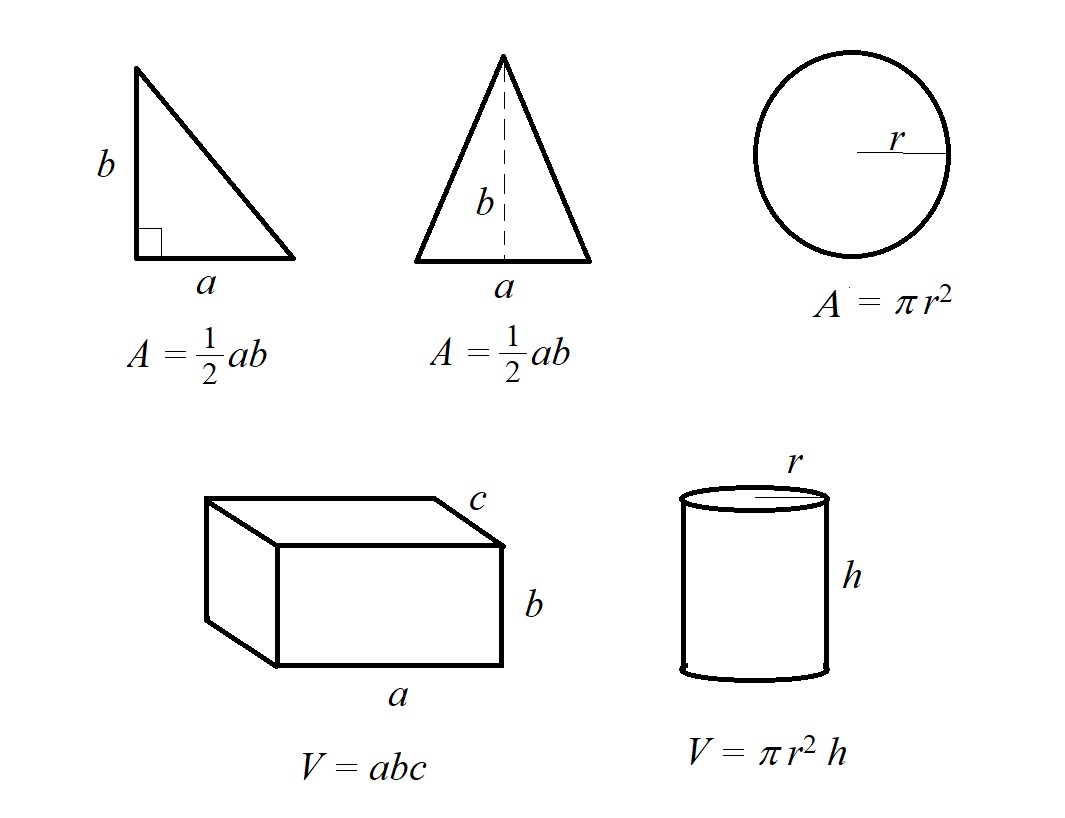
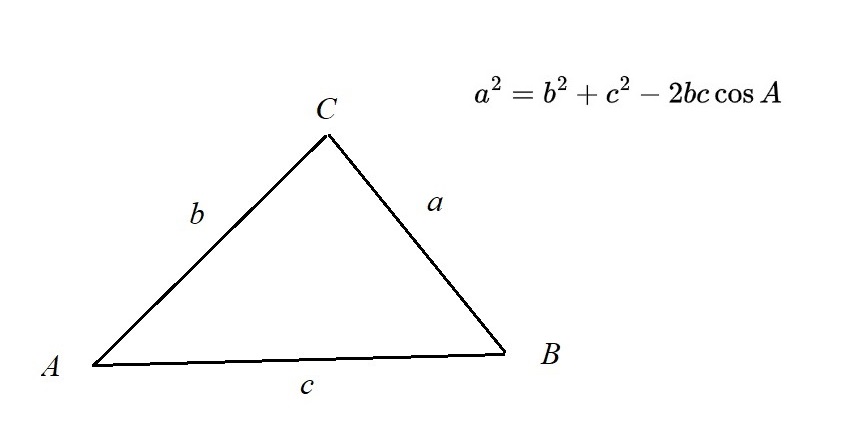
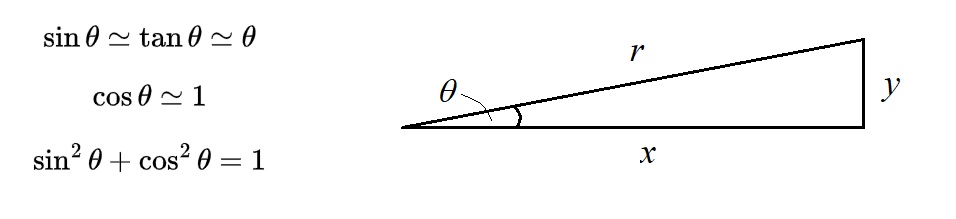
The following is the list of formulae for areas, volumes, angles and sides of common shapes that students need to know.
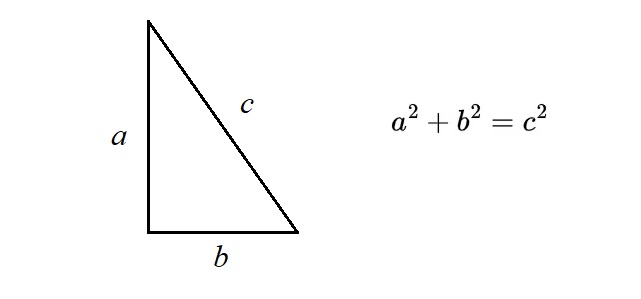

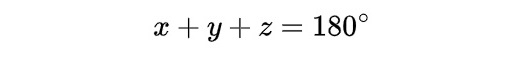
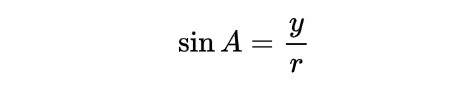
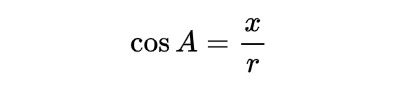
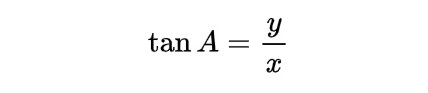
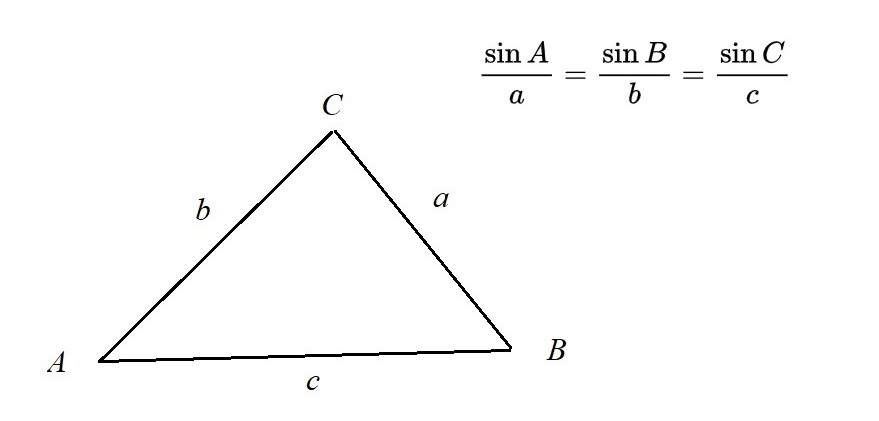
Vectors
The mathematics of vectors is used for physical quantities that have directions. Apart from displacement, velocity and acceleration, we also have momentum and forces.
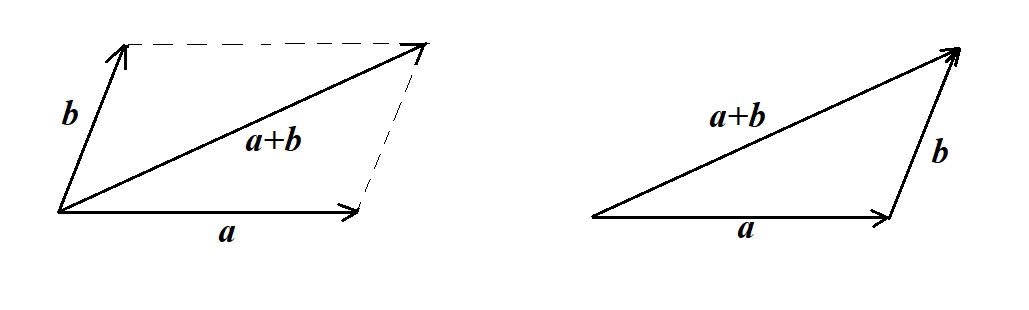
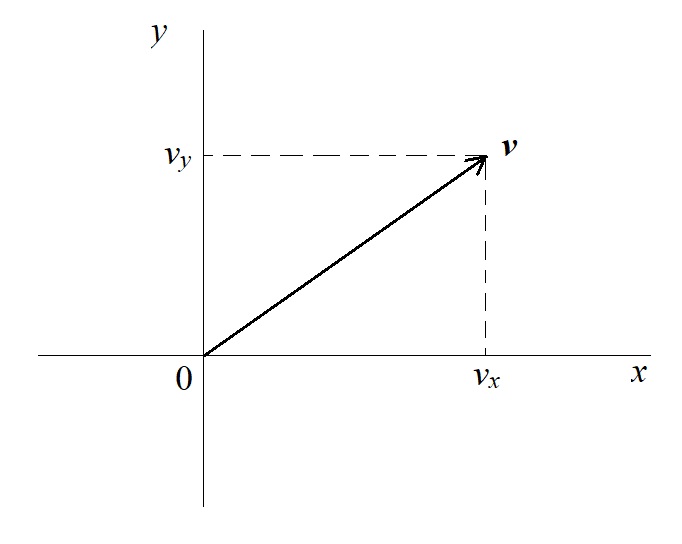
These appear to be topics in Mechanics only. But because forces are also present between electric charges and magnets, vectors naturally have to be used in topics on electricity and nuclear physics also.
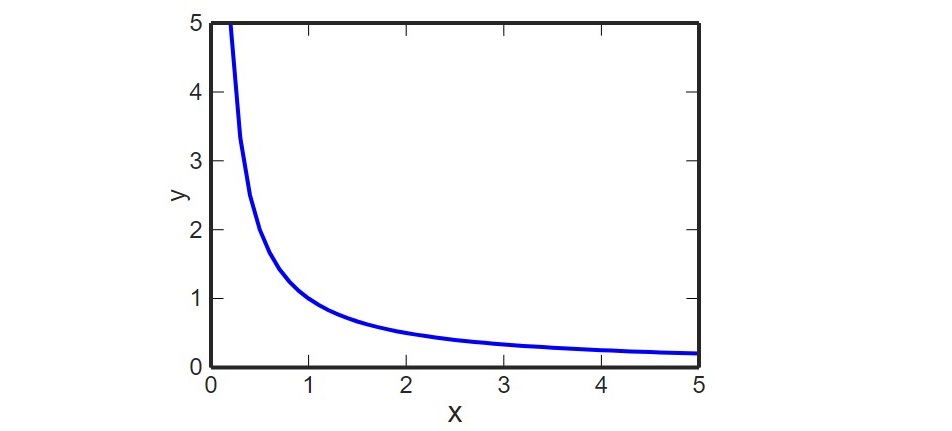
Graphs
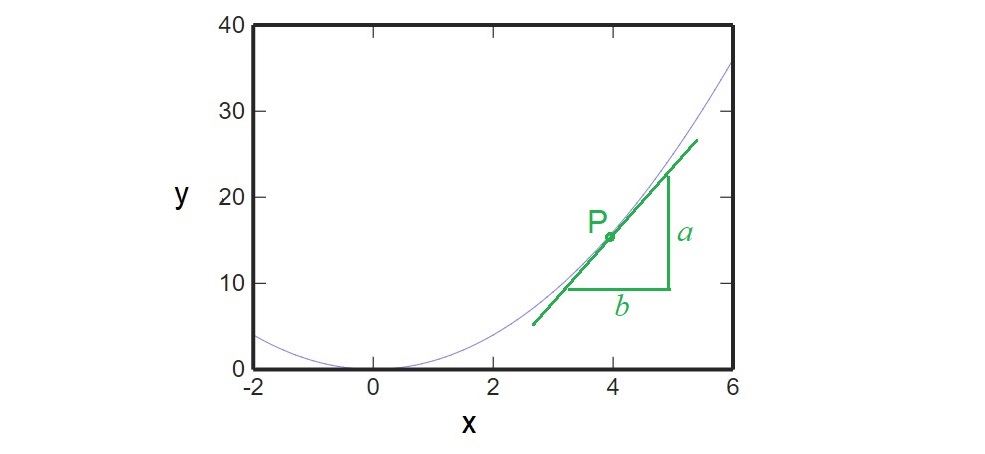
Finally, graphs. The following shows graphs that we need to know in the syllabus. Things we measure on physics can usually be plotted as graphs. And graphs can often give us some new information. For example, gradient of velocity-time graph is acceleration. Area under a force-distance graph is work done. The following are typical graphs we can see in physics.
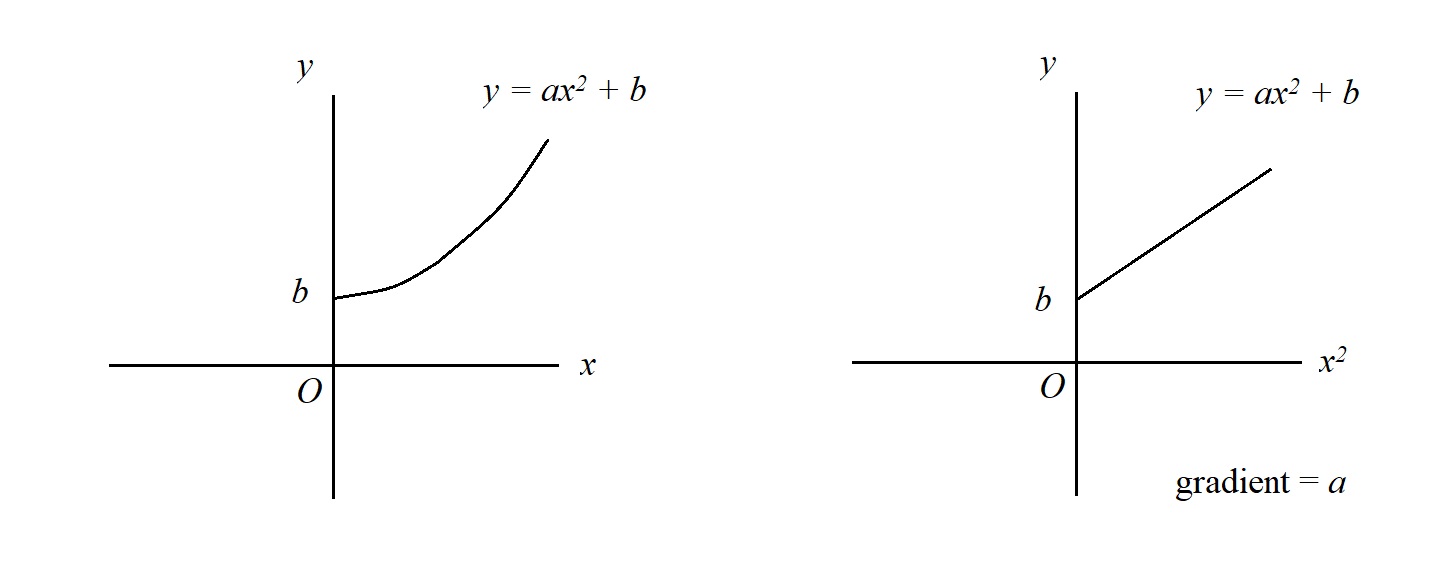
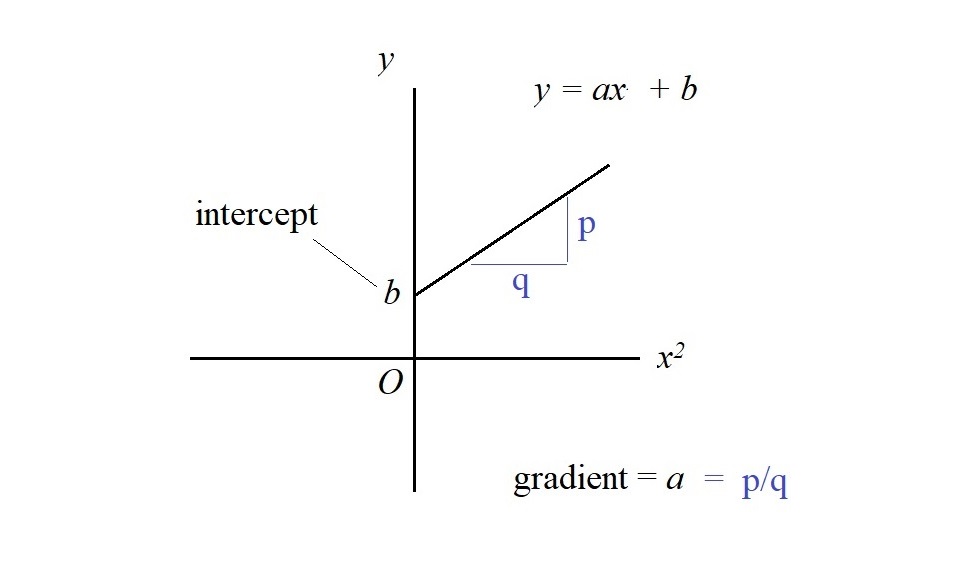
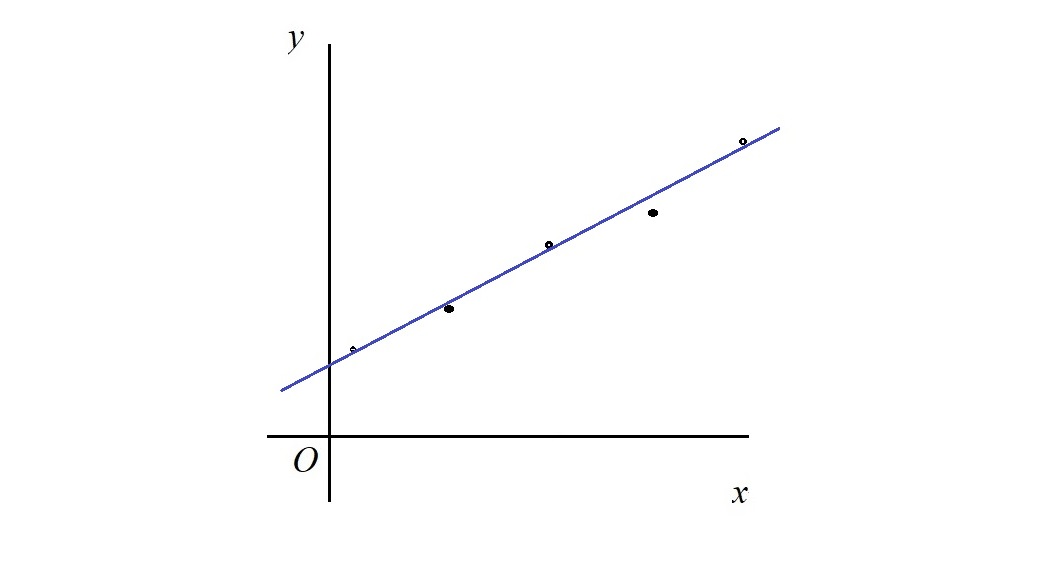
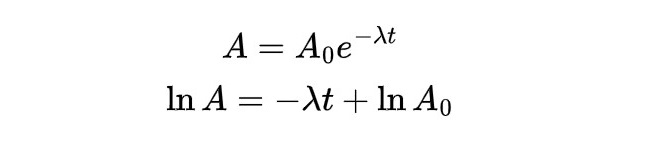
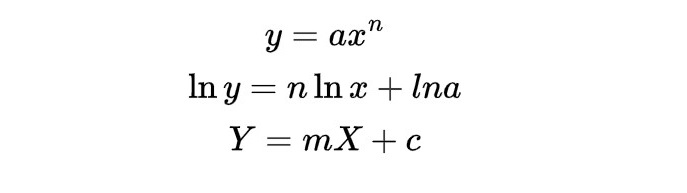
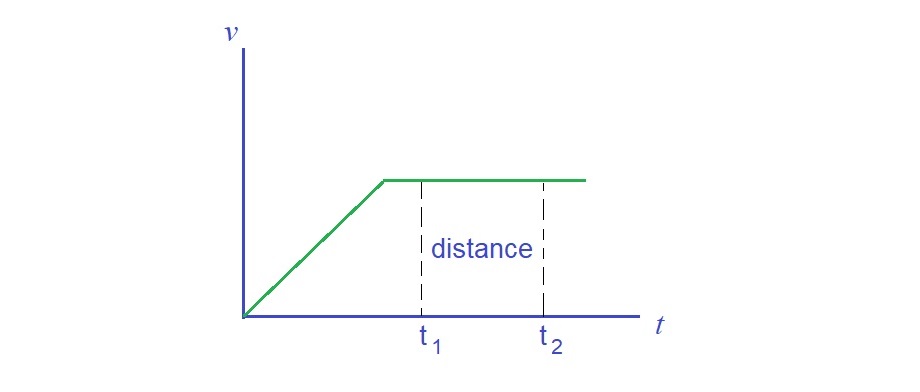
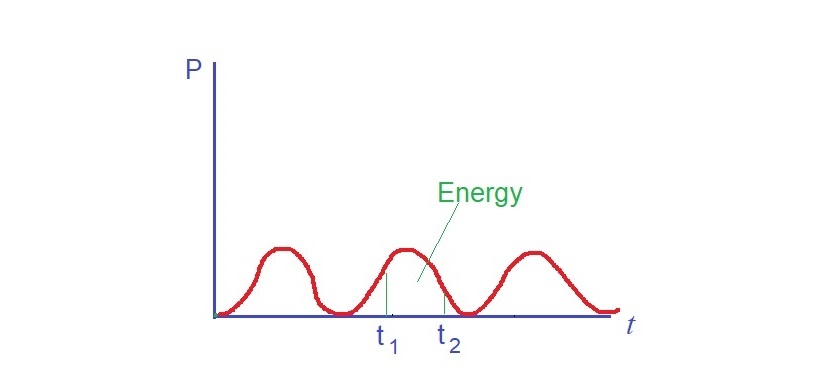
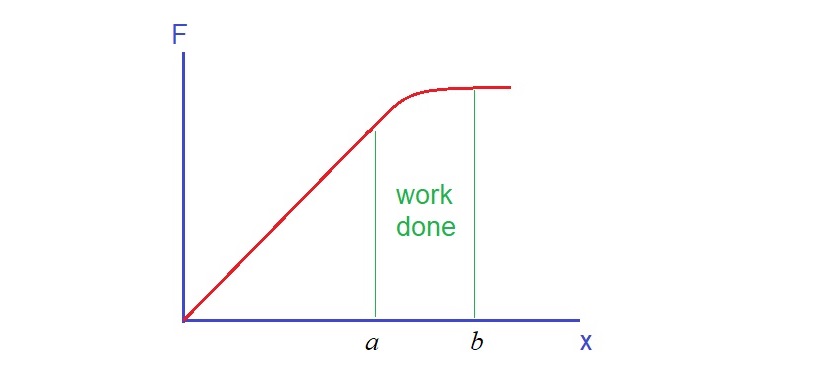
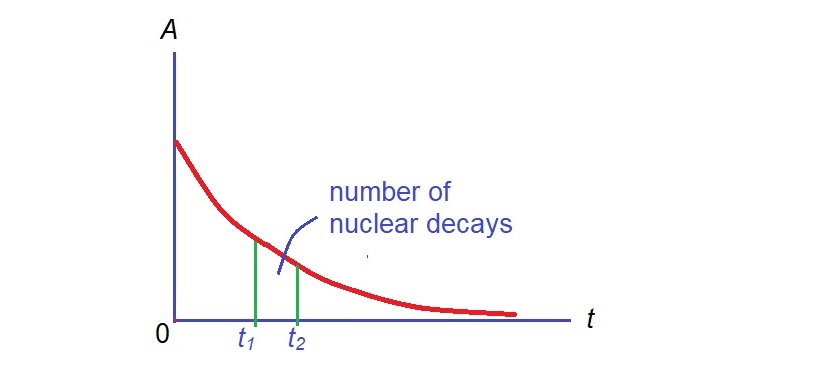
The long list above are all the mathematics you need to know. It does look a bit scary if you are not familiar with these mathematics.
To learn more and improve your maths and physics, come and attend Dr Hock's maths and physics tuition.